记录下第二章(信息的表示与处理)的一些知识 参考IEEE754规范: 四, 非规格数, ±infinity, NaN - 知乎 (zhihu.com)
- 关于tmin Q:48页第二章网络旁注中提到:
C语言中,将TMin32(32位有符号整数的最小值)写成 -2147483647-1。为什么不简单地写成 -2147483648 或者 0x80000000? A:INT_MIN在C语言中表示的是一个有符号整数的最小值。根据C语言标准和二进制补码表示法的规定,INT_MIN的值应该是-2147483648。然而,在《深入理解计算机系统》(CS:APP)第三版中的图CS:APP3e-2.19和问题CS:APP3e-2.21中,我们将TMin32的值写成了-2147483647-1。为什么不直接写成-2147483648或0x80000000呢?
csapp.cs.cmu.edu/3e/was 这篇文章解释了这种写法的原因。这是由于C语言中的两个补码表示法的不对称性和转换规则之间的奇特交互所导致的。当编译器遇到形如-X的数字时,它首先确定X的数据类型和值,然后对其取反。值2147483648对于int类型来说太大了,无法表示为一个int,因为它比TMax32(最大的32位有符号整数)还要大。编译器尝试确定一个能够正确表示这个值的数据类型。根据C语言标准的不同版本,它会从int到long再到unsigned进行尝试,直到找到一个能够表示数字2147483648的数据类型。对于ISO C90版本,它最终找到的数据类型是unsigned,值为2147483648。对于ISO C99版本,它最终找到的数据类型是long long,值为-2147483648。
如果将TMin32写成-2147483648并编译为32位程序,编译器会根据不同的语言版本和数据大小选择不同的数据类型。对于ISO C90版本,它会选择unsigned类型,值为2147483648。对于ISO C99版本,它会选择long long类型,值为-2147483648。
因此,为了避免编译器和语言版本的差异,以及确保TMin32的值在32位程序中被正确表示,我们需要将其写成-2147483647-1。这样可以确保在不同的编译环境下,TMin32的值都能够被正确地表示为一个32位的有符号整数。 这里贴一个知乎帖子:为什么宏INT_MIN要写成-2147483647-1 - 知乎 (zhihu.com) - IEEE 浮点表示
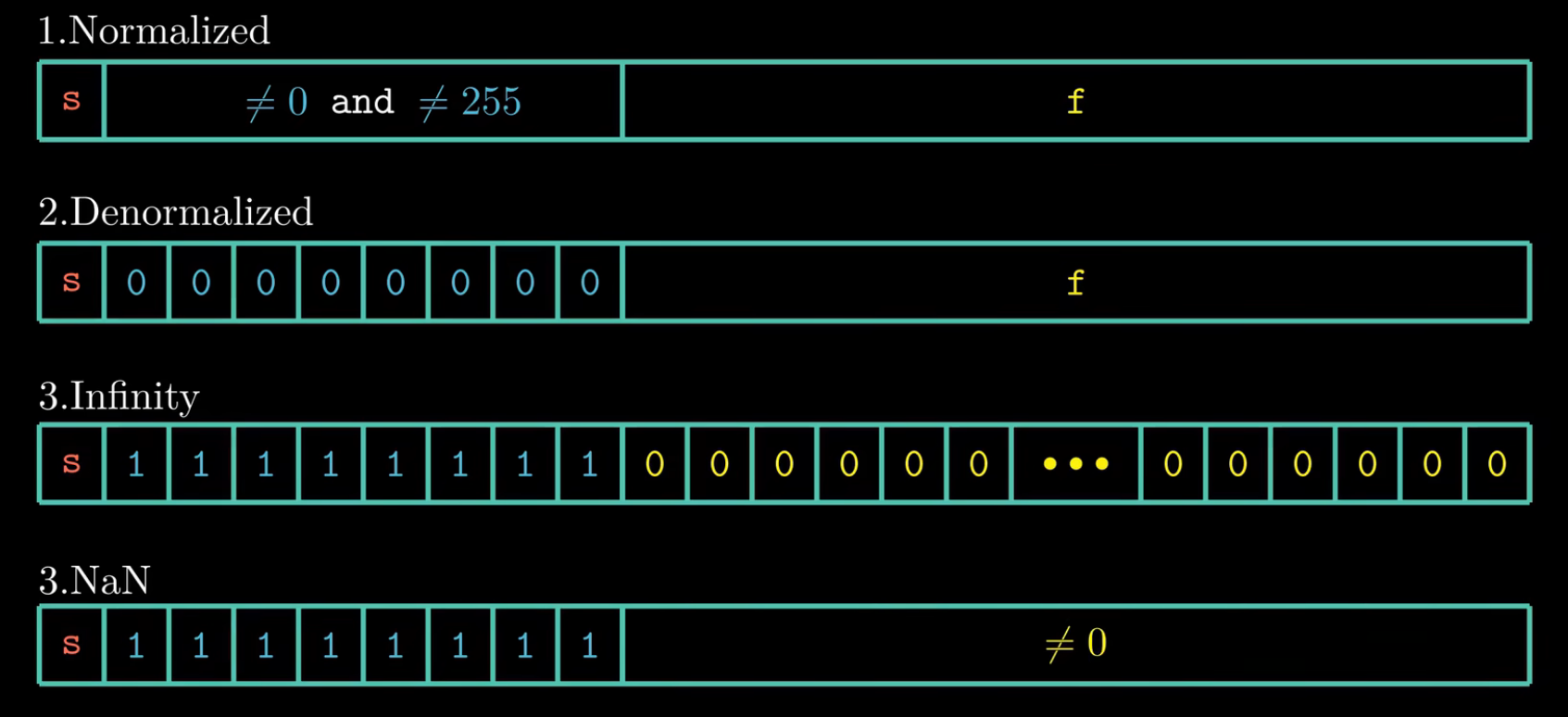
本质是类比科学计数法表示小数。第一位是符号位,0正1负,中间一段是阶码,可以计算出E。为了能够计算负数,IEEE规定将exp的值减去2^段长-1(bias),使得exp段能够以有符号位的形式进行计算。最后一段是尾数位,它代表m的小数部分,frac+1=m。 根据exp的值,被编码的值分成三种不同的情况,这里仅仅讨论单精度情况。

- 第一种不做赘述。
- 第二种非规格化数中,计算M和E的值发生了一些变化: E=1-bias(全0视为1了) M=f(不加1) 非规格化数中m计算方式的更改,使我们可以表示0(规格化数M>=1)其中,+0.0的表示方式是三段全为0,-0.0的表示方式为符号位为1,其余全为0。此外,它还可以表示很接近0的数。
- 第三种特殊值中,当阶码全为0时,表示无穷。当尾数不为全0时,表示NaN(仅仅是一种状态标记) 在浮点数的表示中,对于所有可以表示的非近似值,越靠近0它们越密集。
- 浮点数运算
- 浮点数的舍入:向上,向下,向0,向偶数(二进制0是偶数)
- 浮点数运算不具有结合性,因为舍入会使结果产生偏差
- 关于类型转换,int float double int转float,不会溢出,可能舍入 int或float转换成double,能保留精确数值。 double转换float,可能发生舍入或者溢出 浮点数转换int,值会向0舍入,进一步说会溢出。




Comments | NOTHING